martes, 15 de agosto de 2017
Teoria de conjunto
Teoría de Conjuntos
La teoría de conjuntos y sus fundamentos básicos fueron
desarrollados por George Cantor, un matemático alemán, hacia finales del siglo
XIX. La teoría de conjuntos trata de entender las propiedades de conjuntos que
no están relacionados a los elementos específicos de los cuales están
compuestos. Por ende, tanto los teoremas como los axiomas de la teoría de
conjuntos involucran a conjuntos generales, sin importar que contengan objetos
físicos o números. Existen muchas aplicaciones prácticas de la teoría de
conjuntos.
Función
Desde formular las bases lógicas para la geometría, el
cálculo y la topología, hasta crear álgebra en torno a campos, anillos y
grupos, las aplicaciones de la teoría de conjuntos son comúnmente utilizadas en
campos de las ciencias y las matemáticas como biología, química y física, como
así también en ingeniería eléctrica y computación.
−2 → +4,
|
−1 → +1,
|
0 → 0,
|
|
+1 → +1,
|
+2 → +4,
|
+3 → +9,
|
Matemáticas
Como la teoría es de naturaleza abstracta, tiene funciones y
aplicaciones vitales en el campo de las matemáticas. Una rama de la teoría de
conjuntos es llamada "análisis". El cálculo integral y diferencial
son componentes principales del análisis. La continuidad de una función y los
límites de la misma derivan de la teoría de conjuntos. Estas operaciones
conducen al álgebra de Boole, que es útil para la producción de computadoras y
calculadoras.
p
|
p'
|
1
|
0
|
0
|
1
|
p
|
q
|
p Ù q
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
Teoría de conjuntos generalizada
La teoría de conjuntos generalizada es una teoría
axiomática, y su fácil modificación permite aplicarla a átomos sin estructura
interna. Los conjuntos tienen tanto conjuntos como elementos, y también tienen
átomos como elementos. La teoría de conjuntos generalizada se aplica a pares
ordenados y pares no ordenados que tengan estructura interna.
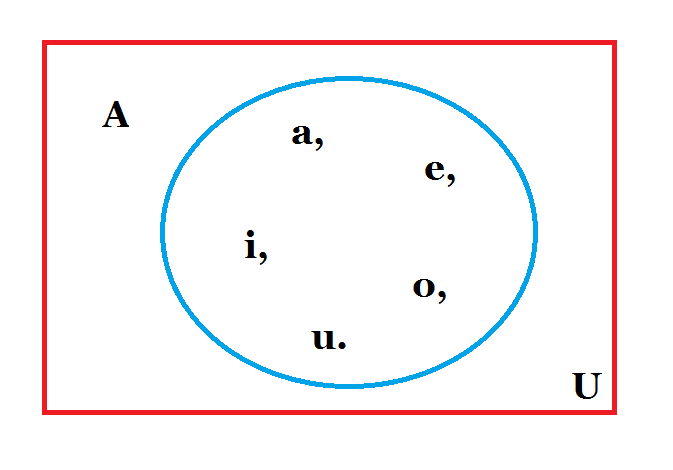
El conjunto V de las vocales puede ser
escrito como:
V = {a, e, i, o, u}
El conjunto C de números enteros impares
positivos menores que diez puede ser expresado por:
C ={ 1, 3, 5, 7, 9 }
Teoría de hiperconjuntos
La teoría de hiperconjuntos es una teoría de conjuntos
axiomática modificada eliminando el Teorema Fundamental y agregando arreglos
posibles de átomos que refuerzan la existencia de conjuntos no del todo bien
establecidos. El axioma no tiene un rol muy importante en codificar objetos
matemáticos. Estos conjuntos son útiles para permitir maneras sencillas de
codificar objetos no bien definidos y circulares.
Teoría de conjuntos constructiva
La teoría de conjuntos constructiva sustituye la lógica clásica con lógica intuitiva. En la teoría de conjuntos axiomática, si los axiomas no-lógicos son formulados de manera precisa, la aplicación de la teoría de conjuntos se conoce como Teoría de Conjuntos Intuitiva. Esta teoría funciona como un método teórico de conjuntos para abordar campos constructivos de la matemática.
Teoría de conjuntos
aplicada a la administración de empresas para selección de personal
¿Cómo se aplica la teoría de
conjuntos en el proceso de selección de personal?
Agrupando elementos o individuos de
características o necesidades que establezcamos en el perfil de cada puesto,
así formaremos unidades de negocios para aprovechar de mejor manera el recurso
humano, considerando siempre los requerimientos más específicos.
Para esto debemos, primero,
establecer las características o cualidades necesarias para todos y cada uno de
los puestos; es así que analizaremos mejor a los postulantes, estableciendo un
balance entre lo que la empresa busca y lo que el colaborador puede ofrecerle a
la misma.
Antecedentes
La selección de personal es un proceso
de previsión para saber cuáles solicitantes tendrán éxito si se les
contrata; es al mismo tiempo, una comparación y una elección. Se basa
en lo que el cargo vacante exige de su futuro ocupante. Así, el primer
cuidado al hacer la selección de personal es conocer cuáles son las
exigencias del cargo que será ocupado.
La selección de personal es una
comparación entre las cualidades de cada candidato con las exigencias del
puesto, y es una elección entre los candidatos comparados (varios candidatos
solicitarán una posición y la empresa contratará al que juzgue más idóneo).
Antiguamente en las organizaciones la
selección se basaba en:
· Observaciones.
· Datos subjetivos (el jefe se engañaba al seleccionar al candidato porque
"le cae bien").
· Intuición.
· Emotividad (en lugar de ser objetivos).
En la actualidad el proceso de
selección de personal, y posterior contratación, se realiza de la siguiente
manera:
1. Hacer
público el perfil del puesto.
2. La
convocatoria.
3. La
selección. Aquí se dan otros pasos:
·
Entrevista inicial.
·
Exámenes psicométricos.
4. Contratación
del personal.
Perfil de puestos
Gerencia.
Actitudes y aptitudes:
·
Ser emprendedor.
·
Capacidad de comunicación.
·
Liderazgo, con motivación para dirigir.
·
Acostumbrado a trabajar en equipo.
·
Iniciativa propia.
Subgerencia.
Actitudes:
·
Alto sentido de responsabilidad y honorabilidad.
·
Capacidad de organización.
·
Actitud positiva en las relaciones interpersonales.
·
Acostumbrado a trabajar bajo presión y por objetivos.
·
Liderazgo.
Jefe de recursos humanos.
Habilidades:
·
Manejo de personal.
·
Liderazgo.
·
Responsabilidad.
Secretaría de gerencia.
·
Práctica.
·
Objetiva.
·
Reservada.
·
Organizada.
Tipos de temperamento
Son bastante conocidos los tipos de
temperamento. En este trabajo los enfocaremos a la funcionalidad en el aspecto
laboral, a la influencia que ejercen en el rendimiento de una persona, y como
ayuda para analizar en qué puesto dentro de la empresa debe estar el
colaborador para lograr un mejor desempeño de acuerdo con sus capacidades y
habilidades.
1.
Colérico:
Positivo: Idóneo para
puestos de liderazgo, motivación y productividad. Orientado al liderazgo
democrático, siempre y cuando no se le exija demasiado planificación analítica.
Se desempeñan correctamente en el comercio, la política, funciones militares,
deportes.
Negativo: Cuando
trabaja con gente, puede llegar a herir deliberadamente y reaccionar
explosivamente, esto puede convertirlo en un líder centrado en la productividad
más que en la gente y con inclinación al liderazgo autocrático.
2.
Flemático:
Positivo: Es eficiente
si se lo exige; es práctico, sencillo y conservador. Hábil, prolijo, planifica
su trabajo antes de empezar. Influye calmado de ánimos. Es confiable en lo que
emprende.
Negativo: Actitud
espectadora, calma y serena de la vida, no se compromete, perezoso. Acepta el
liderazgo a desgano, carece de motivaciones; es indeciso. Se autoprotege de
situaciones comprometedoras. Resiste los cambios.
3.
Sanguíneo:
Positivo: Es conocido
como el optimista, alegre, cálido, extrovertido. Tienen el don de la palabra,
aunque a veces no piensan antes de decir las cosas. Destacan en tareas
hospitalarias, de predicación, de animación o locución. Son excelentes como
actores, anfitriones o vendedores.
Negativo: Su
inestabilidad emocional le afecta en el ámbito laboral porque puede tanto
estallar en irá como llorar con cualquier pretexto; además, no son organizados
y no planean antes de actuar. Su envidiable desenvoltura puede ser para ocultar
su verdadero sentimiento de inseguridad.
4. Melancólico:
Positivo: Es el más
multifacético, cubre la capacidad de análisis, perfeccionismo, talento,
abnegación y sensibilidad. Esta riqueza lo predispone al arte, elige
profesiones complicadas como músico, inventor, artista, filósofo, teólogo,
científico, maestro, teórico.
Negativo: Cuenta el
negativismo, pesimismo y espíritu de crítica. No es muy recomendable para el
liderazgo porque le gusta más que la gente se acerque a él, antes que él
acortar la brecha.
Conclusiones
·
La teoría de conjuntos es particularmente útil para el tratamiento de
los datos recolectados específicamente para cada puesto.
·
Al lograr organizar a la empresa de acuerdo a las aptitudes, actitudes y
temperamentos de cada colaborador se obtiene un mejor clima laboral y trato;
asimismo, se puede mejorar la relación entre cliente-trabajador.
·
Se crean mejores equipos de trabajo, con más eficiencia y más
productividad.
·
La visión en cuanto a selección de personal se vuelve más amplia.
Teoría de
Conjuntos y sus Aplicaciones, "caso en la vida real"
Los compañeros del grupo
Los amigos de las redes sociales
Los contribuyentes menores
Los proyectos de inversión de un proyecto financiero.
Usa el diagrama de Venn para responder las siguientes
preguntas.
1 - Cuantos estudiantes prefieren únicamente Facebook?
2 - Cuantos estudiantes prefieren únicamente twitter?
3 - Cuantos estudiantes usan al menos uno de los dos?
4 - Cuantos estudiantes fueron encuestados?
Los conjuntos sirven:
La idea de agrupar objetos de la misma naturaleza para clasificarlos en “colecciones” o “conjuntos” es parte de la vida diaria de los seres humanos. Por ejemplo, el conjunto de libros de una biblioteca, el conjunto de árboles en un terreno, el conjunto de zapatos en un negocio de venta al público, el conjunto de utensilios en una cocina, etcétera. En todos estos ejemplos, se utiliza la palabra conjunto como una colección de objetos.
Los conjuntos influyen en nuestras vidas en la toma de decisiones sin darnos cuenta, por ejemplo, con el simple hecho de escoger el sabor de un helado de dos sabores de una lista de seis por ejemplo {fresa, mantecado, coco, guanabana,caramelo, chocolate} y elegimos uno de fresa y chocolate , estamos aplicando la teoría de subconjuntos. Entonces al final de una u otra manera está presente la teoría de conjuntos en nuestra vida diaria, ya sea para tomar una decisión o para tener posibles combinaciones de resultados, esta implícito de una manera u otra alguna unión o intersección de procesos o tareas o elecciones.
Los compañeros del grupo
Los amigos de las redes sociales
Los contribuyentes menores
Los proyectos de inversión de un proyecto financiero.
Usa el diagrama de Venn para responder las siguientes
preguntas.
1 - Cuantos estudiantes prefieren únicamente Facebook?
2 - Cuantos estudiantes prefieren únicamente twitter?
3 - Cuantos estudiantes usan al menos uno de los dos?
4 - Cuantos estudiantes fueron encuestados?
Los conjuntos sirven:
La idea de agrupar objetos de la misma naturaleza para clasificarlos en “colecciones” o “conjuntos” es parte de la vida diaria de los seres humanos. Por ejemplo, el conjunto de libros de una biblioteca, el conjunto de árboles en un terreno, el conjunto de zapatos en un negocio de venta al público, el conjunto de utensilios en una cocina, etcétera. En todos estos ejemplos, se utiliza la palabra conjunto como una colección de objetos.
Los conjuntos influyen en nuestras vidas en la toma de decisiones sin darnos cuenta, por ejemplo, con el simple hecho de escoger el sabor de un helado de dos sabores de una lista de seis por ejemplo {fresa, mantecado, coco, guanabana,caramelo, chocolate} y elegimos uno de fresa y chocolate , estamos aplicando la teoría de subconjuntos. Entonces al final de una u otra manera está presente la teoría de conjuntos en nuestra vida diaria, ya sea para tomar una decisión o para tener posibles combinaciones de resultados, esta implícito de una manera u otra alguna unión o intersección de procesos o tareas o elecciones.
TEORIA DE CONJUNTOS
Definiciones:
1.- Conjunto:
es una lista, clase o colección de objetos bien definidos, objetos que, pueden
ser cualesquiera: números, personas, letras, etc. Estos objetos se llaman
elementos o miembros del conjunto.
Ejemplos: { 1, 3, 7, 10}
{x/x2 -3x –2= 0}
{ Inglaterra, Francia,
Dinamarca}
2.-Subconjunto: A es
subconjunto de B si todo elemento de A lo es también de B.
Notación: AÌB Û "x ÎAÞ xÎB
Ejemplo:
El conjunto C =
{1,3,5} es un subconjunto del D = {5,4,3,2,1} ya que todo elemento de C
pertenece al conjunto D.
3.- Conjunto Universal: es
aquel conjunto que no puede ser considerado un subconjunto de otro conjunto,
excepto de si mismo. Todo conjunto se debe considerar un subconjunto del
Conjunto Universal.
Notación: U
Ejemplo:
A = {1,3,5} B = {2,4,6,8}
U =
{0,1,2,3,4,5,6,7,8,9}
4.- Conjunto Potencia: se
denomina conjunto potencia de A, P(A), a la familia de todos los subconjuntos
del conjunto A. Sí el conjunto A tiene n elementos, el conjunto potencia de A
tendrá 2n elementos.
Notación:
Ejemplo:
A = {3,4,5}
P(A)= 23 = 8, lo que significa que
pueden formarse 8 subconjunto de A.
P(A)= { {3}, {4}, {5}, {3,4}, {3,5}, {4,5},
{3,4,5}, f }.
5.- Conjunto Vacío: es aquel que no
posee elementos y es subconjunto de cualquier otro conjunto.
Notación: f = { x / x ¹ x }
Ejemplo:
B= {x/x2 = 4, x es
impar}. B es entonces un conjunto vacío.
6.-Diagrama de Venn: Los diagramas de venn permiten visualizar
gráficamente las nociones conjuntistas y se representan mediante círculos
inscritos en un rectángulo. Los círculos corresponden a los conjuntos dados y
el rectángulo al conjunto universal.
Ejemplo:
A Ì B
7.-Conjuntos Finitos o Infinitos: Los conjuntos serán finitos o infinitos, si
sus elementos son o no factibles de contar.
Ejemplo:
M= {a,e,i,o,u}, M es finito.
N={1,3,5,7...}, N es infinito.
8.- Conjuntos disjuntos: Dos conjuntos son disjuntos si no tienen
elementos comunes.
Gráficamente:
Ejemplo:
A= {1,3,8}, B={2,4,9}; A y B son
conjuntos disjuntos.
OPERACIONES CON CONJUNTOS
1.-Unión de conjuntos: La unión de dos conjuntos A y B es un
conjunto cuyos elementos pertenecen a A o a B.
Notación: AÈB= {x/xÎAÚ xÎB}
Ejemplo
A={3,4,5,8,9} B={5,7,8,9,10}
AÈB={3,4,5,7,8,9,10}
2.- Intersección de conjuntos: La intersección de dos conjuntos A y B, es un
conjuntos cuyos elementos son comunes a
A y B.
Notación: A Ç B= {x / x Î A Ù x Î B}
Gráficamente:

Ejemplo:
A={7,8,9,10,11,12}
B={5,6,9,11,13,14}
A Ç B={9, 11}
3.-Complemento: El complemento de un conjunto A, son todos
los elementos que no están en el conjunto A
y que están en el universo.
Notación: Ac = {x / x ÎU Ù x ÏA}
Ac = U -
A
Gráficamente:
Ejemplo:
U= {1,2,3,...10}
y A={ 3,4,6,7}
Ac=
{1,2,5,8,9,10}
4.- Diferencia de conjuntos: La diferencia de dos conjuntos A y B, es un
conjunto cuyos elementos son aquellos que están en el conjunto A, pero no en el
conjunto B.
Notación: A - B ={x / x ÎA Ù x Ï B}
Ejemplo:
C = {u, v, x, y, z} D = {s, t, z, v, p, q}
C - D = {x, y, u}
5.- Diferencia Simétrica: La diferencia simétrica de dos conjuntos A y
B es un conjunto cuyos elementos son aquellos que están en A, pero no en B,
unidos con aquellos que están en B, pero no en A.
Notación: A D B= {x / x Î A Ù x Ï B} È {x / x ÏA Ù x ÎB}
A D B= ( A - B ) È ( B -A )
Ejemplo:
A= {1,3,4,5,6,7,20,30} B={2,6,20,40,50}
ADB= {1,3,4,5,7,30} È{2,40,50}
ADB= {1,2,3,4,5,7,30,40,50}
6.-Producto cartesiano: El producto cartesiano entre dos conjuntos A
y B es el conjunto de todos los
pares ordenados que tienen como
primera componente un elemento de A y como segundo componente un elemento de B.
Notación: A x B = {(a, b ) / a ÎA Ù b Î B}
Ejemplo:
A= {1,2} B={3,4,5}
A x B =
{(1,3), (1,4), (1,5), (2,3), (2,4), (2,5)}
Observaciones:
1.- n(A) = n Ù n(B) = s Þ n(A x B) = n • s
2.-Si A =
f B = f Û Ax B = f
3.- A x B
¹ Bx A siempre que se
cumpla que A ¹ B
7.- Cardinalidad:
n(AÈB) = n(A) + n(B) – n (AÇB)
n(AÈ(BÈC)) = n(A) + n(B) + n(C) -
n(AÇB) - n(AÇC) – n(BÇC) + n(AÇ(BÇC))
LEYES DE ALGEBRA DE CONJUNTO
1.- Asociatividad:
(AÈB)ÈC = AÈ(BÈC)
(AÇB)ÇC = AÇ(BÇC)
2.- Conmutatividad:
AÈB = BÈA
AÇB = BÇA
3.- Distributividad:
AÈ(BÇC) = (AÈB)Ç(AÈC)
AÇ(BÈC) = (AÇB)È(AÇC)
4.- Absorción:
AÈ(AÇB) = A
AÇ(AÈB) = A
5.- Idempotencia:
AÈA = A
BÇB = B
6.- Identidad:
AÈf = A AÇU = A
AÈU = U AÇf = f
7.-Complemento:
AÈAc = U AÇAc = f
(Ac)c
= A U’= f, f’ = U
8.- Ley
de Morgan:
(AÈB)c = AcÇBc (AÇB)c = AcÈBc
A
– B = AÇBc
Suscribirse a:
Comentarios (Atom)
-
Teoría de Conjuntos La teoría de conjuntos y sus fundamentos básicos fueron desarrollados por George Cantor, un matemático alemán, hacia ...
-
Teoría de Conjuntos y sus Aplicaciones, "caso en la vida real" Los compañeros del grupo Los amigos de las redes sociales Los...