Teoria de conjunto

Teoría de Conjuntos

La teoría de conjuntos y sus fundamentos básicos fueron desarrollados por George Cantor, un matemático alemán, hacia finales del siglo XIX. La teoría de conjuntos trata de entender las propiedades de conjuntos que no están relacionados a los elementos específicos de los cuales están compuestos. Por ende, tanto los teoremas como los axiomas de la teoría de conjuntos involucran a conjuntos generales, sin importar que contengan objetos físicos o números. Existen muchas aplicaciones prácticas de la teoría de conjuntos.

Función

Desde formular las bases lógicas para la geometría, el cálculo y la topología, hasta crear álgebra en torno a campos, anillos y grupos, las aplicaciones de la teoría de conjuntos son comúnmente utilizadas en campos de las ciencias y las matemáticas como biología, química y física, como así también en ingeniería eléctrica y computación.

−2 → +4,	−1 → +1,	0 → 0,
	+1 → +1,	+2 → +4,	+3 → +9,

Matemáticas

Como la teoría es de naturaleza abstracta, tiene funciones y aplicaciones vitales en el campo de las matemáticas. Una rama de la teoría de conjuntos es llamada "análisis". El cálculo integral y diferencial son componentes principales del análisis. La continuidad de una función y los límites de la misma derivan de la teoría de conjuntos. Estas operaciones conducen al álgebra de Boole, que es útil para la producción de computadoras y calculadoras.

p	p'
1	0
0	1

p	q	p Ù q
1	1	1
1	0	0
0	1	0
0	0	0

Teoría de conjuntos generalizada

La teoría de conjuntos generalizada es una teoría axiomática, y su fácil modificación permite aplicarla a átomos sin estructura interna. Los conjuntos tienen tanto conjuntos como elementos, y también tienen átomos como elementos. La teoría de conjuntos generalizada se aplica a pares ordenados y pares no ordenados que tengan estructura interna.

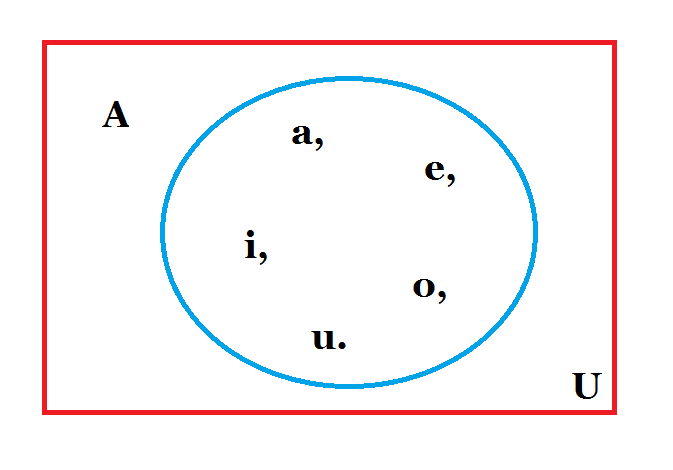
El conjunto V de las vocales puede ser escrito como:

V = {a, e, i, o, u}

El conjunto C de números enteros impares positivos menores que diez puede ser expresado por:

C ={ 1, 3, 5, 7, 9 }

Teoría de hiperconjuntos

La teoría de hiperconjuntos es una teoría de conjuntos axiomática modificada eliminando el Teorema Fundamental y agregando arreglos posibles de átomos que refuerzan la existencia de conjuntos no del todo bien establecidos. El axioma no tiene un rol muy importante en codificar objetos matemáticos. Estos conjuntos son útiles para permitir maneras sencillas de codificar objetos no bien definidos y circulares.

Teoría de conjuntos constructiva

La teoría de conjuntos constructiva sustituye la lógica clásica con lógica intuitiva. En la teoría de conjuntos axiomática, si los axiomas no-lógicos son formulados de manera precisa, la aplicación de la teoría de conjuntos se conoce como Teoría de Conjuntos Intuitiva. Esta teoría funciona como un método teórico de conjuntos para abordar campos constructivos de la matemática.